🧙‍♀️✨ Qubits Neuron Class 🚀🌌

This bespoke Python class has two aims:

1. Code that models qubits
2. A course that prepares computer scientists for qubits

A nice starting place is in the notations used in common formulas. Later in this document, Dirac Notation, sometimes called Bra-ket Notation (

0⟩,

1⟩), will be introduced. It will be helpful to have worked with linear algebra, probability, and a bit of calculus.

Qubit Example

This example demonstrates how to visualize a single qubit on the Bloch sphere using the BlochSphere and Qubit classes in Python.

Create a qubit with equal superposition state

 qubit = Qubit(a=1/np.sqrt(2), b=1/np.sqrt(2)) 

Plot the qubit on the Bloch sphere

 qubit.plot_qubit() 

This code initializes a qubit in an equal superposition state and visualizes it on the Bloch sphere.

Goal State

Hamiltonian Graph with Super Clusters

The goal is to simulate quantum holographic properties using a complex neural network.

Full Process

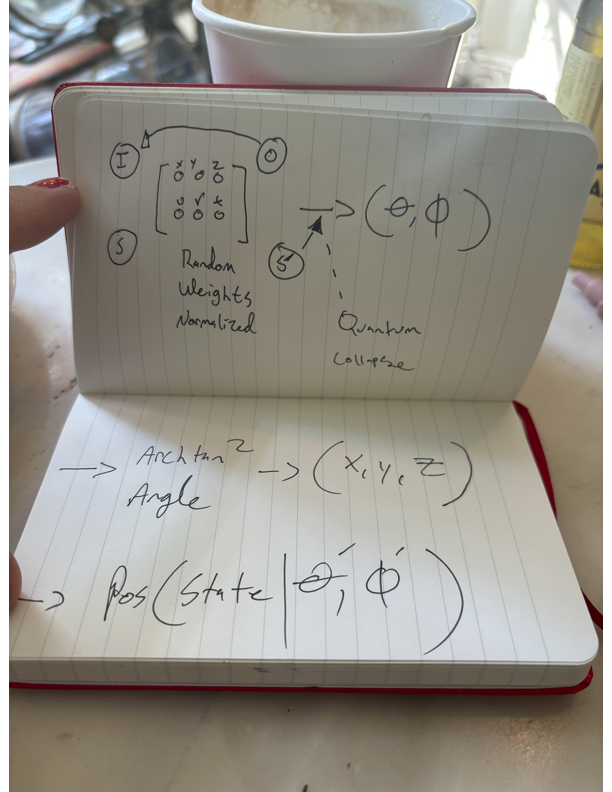
What is a Qubit? 🧩

A qubit is the basic unit of quantum information, just like a bit in classical computing. However, qubits are magical because they can be in a superposition of states! Kind of like gender 🧙‍♀️✨

In simple terms:

• A classical bit can be either 0 or 1.
• A qubit can be in a state |0⟩, |1⟩, or any superposition α|0⟩ + β|1⟩ where α and β are complex numbers, just like us humans.
• α (alpha) is the amplitude for the state |0⟩.
• β (beta) is the amplitude for the state |1⟩.
• Note: This is in Hilbert Space💖
• Note: Layer class demands a Hamiltonian Graph as the lower level diameter aka graph connectivity
• Note: Ideally and for ease sake this is an Orthonormal relationship, which you can't find in Brooklyn

Source: 1.) MIT: A Gentle Introduction to Quantum Computing

Source: 2.) MIT: Holographic Quantum Matter

Braket Notation in Quantum Mechanics 🧙‍♀️🔮

In quantum mechanics, bra-ket notation is essential for representing quantum states and operations.

• Ket |α⟩: Represents a quantum state vector. Example: |α⟩ could denote the state of a particle. 🌌
• Bra ⟨β|: The conjugate transpose of a ket, representing the dual vector. 🔄
• Inner Product ⟨β|α⟩: Probability amplitude between states |β⟩ and |α⟩. ✨
• Outer Product |α⟩⟨β|: Operator that projects onto the state |α⟩. 🌀

Example in a qubit system:

• Kets: |0⟩, |1⟩
• Bras: ⟨0|, ⟨1|
• Inner Product: ⟨0|1⟩ = 0 (orthogonality) 🌠
• Outer Product: |0⟩⟨0| (projection operator) 🌙

Measuring a Qubit 🔍

When we measure a qubit, we "collapse" its superposition to one of the basis states:

• The probability of collapsing to |0⟩ is |α|².
• The probability of collapsing to |1⟩ is |β|².

How It Works

1. State Vector: The qubit is in a state α|0⟩ + β|1⟩.
2. Probabilities: Calculate the probabilities |α|² and |β|².
3. Random Choice: Use these probabilities to randomly choose the measurement outcome.

Example in Python

import numpy as np

class Ket:
    def __init__(self, alpha, beta):
        self.state_vector = np.array([alpha, beta], dtype=complex)

    def measure(self):
        probabilities = np.abs(self.state_vector) ** 2
        return np.random.choice([0, 1], p=probabilities)

# Example usage
alpha = 1/np.sqrt(2)
beta = 1/np.sqrt(2)
ket_instance = Ket(alpha, beta)
measurement_result = ket_instance.measure()
print(f"Measurement result: {measurement_result}")